2009-10-20 [長年日記]

■ [Haskell] The Typeclassopediaを訳しました

The Monad.ReaderのIssue 13に掲載されたThe Typeclassopediaという記事が、Functor, Monad, Monoid, Applicative, Foldable, Traversable, Arrowといったような型クラスについて良くまとまっていて、そのあたりを知りたい時の取っ掛かりになりそうだったので翻訳してみました。

作者のBrent Yorgeyさんからも許可がいただけたので公開します。翻訳に慣れていないので変な日本語（特に専門用語の日本語訳はかなり怪しい）があったり、そもそも間違っていたりするかもしれませんので、何か見つけたらコメントを頂けると助かります。

■ [Haskell] The Typeclassopedia

by Brent Yorgey <first initial last name at cis.upenn.edu>

標準Haskellライブラリには、代数や圏論に裏打ちされた数多くの型クラスが用意されています。流暢なHaskellハッカーになるためには、これら全てに根本的に慣れ親しんでいる必要がありますが、慣れ親しむためには、しばしば山ほどのチュートリアルやブログの記事、メーリングリストのアーカイブ、IRCのログをくまなくチェックする必要があります。

この記事の目的は、標準の型クラスについてしっかり理解したいと望んでいるHaskell学習者のはじめの一歩となることです。それぞれの型クラスの基本的なことを、例や注釈と更なる読み物への参照とともに紹介します。

序論

いままでこんなことを考えたことがありませんか?

  • いったいモノイドとは何で、モナドとは何が違うのか?
  • ようやくParsecをdo記法と共に使うやり方がわかったのに、代わりにApplicativeを使うべきだと言われた。それは何?
  • #haskell IRCチャンネルで、誰かが(***)を使っていたので、lambdabotにその型を尋ねたら、回りくどくてわかりにくい一行に収まらないような型が表示された。さらには、誰かがfmap fmap fmapを使ったので、訳が分からなくなった。
  • すごく複雑なことのやり方を尋ねたら、みんながzip.ap fmap.(id &&& wtf)みたいなのをタイプし始め、びっくりすることにそれらはちゃんと動いた! それはともかく、そんなものを2秒で思いつく方法なんてあるわけがないから、彼らはロボットに違いないと思う。

そんなことを考えたことがあれば、これ以上探す必要はありません。あなたも彼らと同じように簡潔でエレガントで慣用句的なHaskellのコードを書いたり理解したりすることができます。

エキスパートなHaskellハッカーになるための二つの鍵があります。一つ目は型を理解すること。二つ目は、それぞれの型クラス、そしてそれらと他の型クラスとの関係について、たくさんの例に馴染みながら深い洞察を得ることです。

一つ目の鍵は特に重要です。型シグニチャを我慢強く学習すれば、深い秘密を暴くことができます。逆に、コードの中で型について意識しない人は、永遠に確信が持てない運命なのです。「ああ、これはコンパイルできない…たぶん、このfmapが良くないんだろう。いや、ちょっと待て…おそらくどこかに(.)がもう一つ必要なんじゃないか?」

二つ目の鍵、つまり例に基づいて深い洞察を得ること、もまた重要ですが、さらに達成するのは難しいことです。この記事の主要なゴールは、あなたをそのような洞察を得る軌道に乗せることです。しかし、

Haskellに王道なし ---Euclid

この記事ははじめの一歩に過ぎません。なぜならば、良い洞察は猛勉強からしか得られず、良いメタファー[1]を学ぶことからは得られないからです。この記事の全てを読んで理解したとしても、まだ険しい旅が待っています。しかし、良いはじめの一歩は、時に大きな違いを生み出します。

この記事がHaskellのチュートリアルではないことは明記しておいた方が良いでしょう。読者は、標準Preludeや型システム、データ型、型クラスなどのHaskellの基礎について馴染みがあると仮定しています。

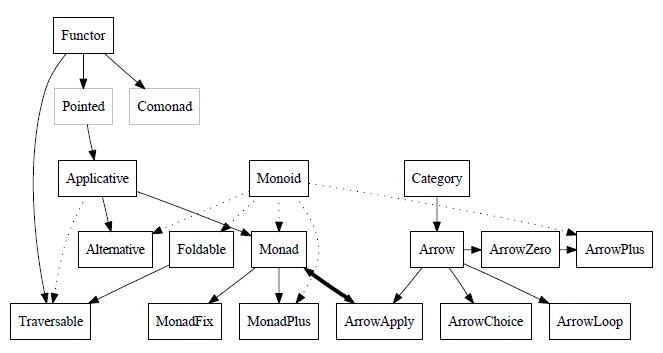
図1: 標準Haskell型クラス間の関係
図1: 標準Haskell型クラス間の関係

図1はこれから私たちが議論する型クラスと、それらの間の関係を表しています。実線の矢印は、一般的なものから具体的なものに引かれています。つまり、もしFooからBarへの矢印があれば、それは全てのBarはFooである（もしくは、Fooであるべきであるか、Fooにすることができる）という意味です。破線の矢印はその他の何らかの関係を表しています。双頭の実線の矢印は、MonadとArrowApplyが同等のものであることを表しています。PointedとComonadは、標準Haskellライブラリに（まだ）入っていないので、灰色になっています（それらは、category-extraライブラリ[2]にあります）。

始める前にもう一つの注意があります。"type class"が"typeclass"と一つの単語として書かれているのを見たことがありますが、ここではっきりさせておきましょう。正しい綴りは二つの単語を使います（この記事のタイトルにも関わらず）。このことは、例えばHaskell 98 Revised Report[3]や、型クラスに関する初期の論文[4,5]、そしてHudakらのHaskellの歴史[6]を見れば明らかです。

それではもっとも単純な型クラスであるFunctorから始めましょう。

Functor

Functorクラスは、Haskellのライブラリの中で、もっとも基本的でどこにでもある型クラスです。Functorは、コンテナ内の各要素に対して関数を適用することができるような何らかの「コンテナ」である、というのが単純な洞察です。例えば、リストは要素のコンテナで、mapを使って各要素に関数を適用することができます。二分木も要素のコンテナで、木の中の各要素に関数を再帰的に適用する方法は簡単に思いつきます。

別の洞察では、Functorは何らかの「計算の文脈」を表します。この洞察は一般的にはもっと有用ですが、あまりにも一般的すぎて説明するのがもっと難しいものです。後で示すいくつかの例が、文脈としてのFunctorという見方を明確にするのを助けてくれるはずです。

最後になりますが、とはいってもFunctorは単にそのように定義されたものに過ぎません。おそらく上の二つの洞察にぴったりそぐわないFunctorのインスタンスの例はたくさんあります。賢い生徒は定義と例に注目し、特定のメタファーから学びすぎないようにするでしょう。洞察はいつかそれそのものとして得ることができます。

定義

リスト5は、Functorの型クラスの定義を示しています。FunctorはPreludeから公開されているので、使うために特別なインポートは必要ありません。

class Functor f where
  fmap :: (a -> b) -> f a -> f b

リスト5: Functor型クラス

まず、fmapの型シグニチャのf aとf bを見れば、fが単なる型ではないことがわかります。これは他の型を引数に取る型構築子なのです（もっと正確な言い方をするならば、fの種は* -> *でなくてはなりません）。例えば、Maybeはそのような型構築子です。Maybeはそれ自体は型ではなく、Maybe Integerのように、他の型が引数として必要です。ですから、instance Functor Integerということはできませんが、instance Functor Maybeということはできます。

さて、fmapの型を見てみましょう。fmapは、aからbへの任意の関数とf a型の値を取り、f b型の値を出力します。コンテナという見方からすると、fmapは、コンテナの構造を変えることなく、コンテナの各要素に対して関数を適用すると言うことができます。文脈という見方からすると、fmapは文脈を変えることなく値に関数を適用すると言えます。いくつかの具体的な例を見てみましょう。

インスタンス

先に述べたように、リストの構築子である[]はファンクタです。標準のリスト関数であるmapを使って、リストの各要素に関数を適用することができます。Maybe型構築子も同様にファンクタで、ひとつの要素を保持しているかも知れないコンテナをあらわします。fmap g関数はNothingに対しては何もせず（gが適用され得る要素がありません）、単にJustのひとつの要素に対してgを適用します。あるいは、文脈という解釈では、リストのファンクタは非決定的な選択の文脈を表します。つまり、リストは、いくつかの可能性（リストの要素）から非決定的に選ばれるひとつの値を表している、と考えられます。同様にMaybeのファンクタは失敗が起こりうる文脈を表現します。これらのインスタンスは、リスト6に示されています。

instance Functor [] where
  fmap _ []     = []
  fmap g (x:xs) = g x : fmap g xs
  -- もしくは単にfmap = mapとも言えます

instance Functor Maybe where
  fmap _ Nothing  = Nothing
  fmap g (Just a) = Just (g a)

リスト6: 二つの単純なFunctorインスタンス

余談としてですが、よく見るであろう慣用句的なHaskellのコードでは、fは任意のFunctorと任意の関数の両方をあらわすのに使われます。このチュートリアルでは、fはFunctorをあらわすのに使い、関数はgやhであらわしますが、混乱しないように気をつけてください。実際には、fが何を表すかは、型の一部として現れたか、コードの一部として現れたかという文脈から常に明らかです。

Haskellの標準ライブラリには他にもFunctorのインスタンスがあります。いくつかを取り上げます。

  • Either eはFunctorのインスタンスです。Either e aはa型の値かe型の値のどちらかを含むコンテナを表します（しばしば何らかのエラーを表します）。起こりうる失敗を表すという点でMaybeと似ていますが、失敗に関する追加の情報を持つことができます。
  • ((,) e)はe型の「注釈」を実際の値と共に保持するコンテナをあらわします。
  • ((->) e)、つまりe型の値を引数に取る関数はFunctorです。(1+)のような演算子セクションと同様に(e ->)のように書けるともっと明確なのですが、このような書き方は許されていません。しかし、(e ->)だと考えてもらってかまいません。コンテナとしては、(e -> a)は、e型の値で指定される、（無限に存在するかもしれない）a型の値の集合を表します。あるいは、もっと役に立つ方法として、(e ->)は型eの値が読み込み専用として参照できる文脈だと考えることができます。このことは、((->) e)が時々リーダーモナドと言われる訳でもあります。詳細は後ほど。
  • IOはFunctorです。IO a型の値は、型aの値を生成する、I/Oを伴うかも知れない計算を表します。もし、mが何らかのI/Oを伴って値xを計算するのならば、fmap g mは同じI/Oを伴い値g xを計算します。

containersライブラリ[8]にある（Tree, Map, Sequence, Streamのような）沢山の標準の型はFunctorのインスタンスです。注意すべき例外はSetで、（数学的には確かにファンクタなのですが）HaskellではFunctorにすることができません。これは、Setが要素に対してOrd制約を必要とするからです。fmapはあらゆる型aとbに対して適用できなくてはなりません。

Either e、((,) e)、((->) e)のFunctorのインスタンスを実装してみるのは良い練習になります。

法則

Haskell言語が関知する限りにおいては、Functorに対する要件は正しい型でfmapを実装することだけです。しかし、理にかなったFunctorのインスタンスは全て同様にファンクタ法則を満たします。この法則は、数学におけるファンクタの定義の一部です。リスト7に示される二つの法則を合わせると、fmap gがコンテナの構造を変えず、要素だけを変更することが保証されます。同等に、そしてもっと単純に、これらの法則はfmap gが文脈を変えずに値を変えることを保証します。

fmap id = id
fmap (g . h) = fmap g . fmap h

リスト7: Functor法則

最初の法則は、コンテナの各要素に恒等関数を適用しても変化が無いことを意味します。二つ目の法則は、二つの関数を合成した関数をコンテナの各要素に適用するのは、初めに一つ目の関数を適用し、次に二つ目の関数を適用するのと同じであることを意味します。

例として、リスト8に示したコードは、正当なFunctorのインスタンス（型チェックができる）ですが、ファンクタ法則を破っています。なぜだかわかりますか?

instance Functor [] where
  fmap _ [] = []
  fmap g (x:xs) = g x : g x : fmap g xs

リスト8: 法則に従わないFunctorインスタンス

有能なHaskellerは、リスト8のコードを、ぞっとする大嫌いなものとして排除するでしょう。

洞察

fmapについて考える根本的な方法が二つあります。一つ目は既に触れた方法です。fmapは、関数とコンテナの二つの引数をとり、関数をコンテナの「内部」に適用して新しいコンテナを生成します。あるいは、fmapを文脈内の値に（文脈を変更せずに）関数を適用することだと考えることもできます。

しかし、他の全ての「ひとつ以上の引数を取る」Haskellの関数と同様に、fmapは実際にはカリー化されています。つまり、実際には二つの引数を取るのではなく、ひとつの引数を取って関数を返します。強調するために、fmapの型を追加の括弧をつけて、fmap :: (a -> b) -> (f a -> f b)と書くことができます。このような形で書くと、fmapが「普通の」関数（g :: a -> b）を、コンテナ・文脈に対して作用する関数（fmap g :: f a -> f b）に変換していることが明らかになります。この変換はしばしば持ち上げと呼ばれます。つまり、fmapは関数を「普通の世界」から「fの世界」に持ち上げるわけです。

更なる読み物

ファンクタの概念の背後にある圏論について読むのには、圏論についてのHaskell wikibookのすばらしいページ[9]が良い取っ掛かりとなるでしょう。

Pointed

Pointed型クラスは、基点付きファンクタを表します。この型クラスは、実際には標準ライブラリには含まれません。しかし、標準ライブラリに含まれうるものですし、この型クラスはApplicativeやMonadのような他の型クラスを理解する助けとなるので、しばらく標準に含まれているとしましょう。

Functorがあるとして、Pointedクラスは値を「デフォルトの文脈」に入れる追加の機能を表します。しばしば、このことはただひとつの要素だけをもったコンテナを作成することに対応しますが、実際にはもっと一般的なものです。リスト9にこの型クラスの宣言を示します。

class Functor f => Pointed f where
  pure :: a -> f a     -- またの名を、singleton, return, unit, point

リスト9: Pointed型クラス

ほとんどの標準のFunctorインスタンスは、Pointedのインスタンスでもあります。たとえば、MaybeのPointedインスタンスでは、pure = Justになります。リストの実装は沢山ありえますが、もっとも自然なものは、pure x = [x]です。((->) e)に対しては、考えてみてください（単に型に従いましょう）。

PointedでないFunctorの例としては、((,) e)があります。もし、pure :: a -> (e, a)を実装しようとすれば、それがなぜだかわかるはずです。型eは完全に任意なので、何も無いところから型eの値を作り出すことはできないからです。しかし、後で見るように、((,) e)は、eに、型eのデフォルトの値を生成することができるような追加の制約を課すならばPointedにすることができます（最も一般的な解決方法は、eをMonoidのインスタンスにすることです）。

Pointedクラスは、リスト10で示されるようなただひとつの法則を持ちます。

fmap g . pure = pure . g

リスト10: Pointed法則

しかし、この法則について心配する必要はありません。この法則はパラメトリシティ[11]によって保証される、いわゆる「ただで手に入る定理」です。この法則に従わないPointedのインスタンスを書くことは不可能です。

Applicative

やや新しく標準Haskell型クラスの殿堂に追加された、アプリカティブファンクタは、ちょうどFunctorとMonadの間に位置する抽象化を表し、McBrideとPaterson[12]によって初めて述べられました。McBrideとPatersonの古典的論文のタイトルである、Applicative Programming with Effectsは、Applicative型クラスの裏にある洞察に関するヒントを与えてくれます。この型クラスは、関数的に純粋な方法で行われるある種の「副作用のある」計算をカプセル化し、「アプリカティブ」なプログラミングスタイルを推し進めます。正確にどんなことを意味するのかは、この後で明らかにされます。

定義

Applicativeクラスは、ひとつの機能をPointedファンクタに追加します。Functorクラスが「通常の」関数を計算の文脈の関数に持ち上げることができることを思い出してください。しかし、fmapはそれ自体が文脈の中にある関数を、他の文脈にある値に適用することはできません。Applicativeはまさにそのためのツールを与えてくれます。リスト11は、Control.Applicativeで定義されている、Applicative型クラスの宣言を示しています。全てのApplicativeは同時にFunctorでなくてはならないことに注意してください。実は、後で見るように、fmapはApplicativeのメソッドを使って実装することができますので、好む好まざるにかかわらず、すべてのApplicativeはファンクタになります。Functor制約があるのでごまかしはできません。

class Functor f => Applicative f where
  pure :: a -> f a
  (<*>) :: f (a -> b) -> f a -> f b

リスト11: Applicative型クラス

いつものように、(<*>)の型シグニチャを理解するのは必須です。(<*>)を考えるにあたってもっとも良い方法は、(<*>)の型が($)の型に似ているけれど全てがfの中に閉じ込められていることに注目することです。別の言い方をすると、(<*>)は、単に計算の文脈における関数適用に過ぎないのです。(<*>)の型はまたfmapの型にとてもよく似ています。たった一つの違いは、最初の引数が(a -> b)という「普通の」関数ではなくて、f (a -> b)という文脈の中の関数であることです。

もちろん、pureはさらに見慣れたものです。もし既にPointed型クラスがあれば、Applicativeはリスト12に示されたように定義されるでしょう。

class Pointed f => Applicative' f where
  (<*>) :: f (a -> b) -> f a -> f b

リスト12: Pointedを使ったApplicativeの別の定義
法則

Applicativeのインスタンスが満たすべき法則[11,12]はいくつかありますが、洞察を養うにはそのうちのひとつが重要です。なぜなら、その法則がApplicativeがFunctorとどのように関連するかを明確にするからです（他の4つは、主にpureがその名前の通りに振舞うことの正確な意味を明確にします）。リスト13にこの法則を示します。

fmap g x = pure g <*> x

リスト13: ApplicativeのFunctorに対する関係に関する法則

この法則は、純粋な関数gを文脈xに対してマップするのは、初めにpureを使用してgを文脈に注入してからそれを(<*>)を使ってxに適用するのと同じである、ということです。別の言い方をすると、fmapは二つのもっと原始的な操作、つまり文脈への注入と、文脈内での適用、に分解することができます。Control.Applicativeモジュールは、同様に(<$>)をfmapの別名として定義しているので、上記の法則は、g <$> x = pure g <*> xと表現することもできます。

インスタンス

Functorのインスタンスである標準型のほとんどはApplicativeのインスタンスです。

Maybeは簡単にApplicativeのインスタンスにすることができます。そのようなインスタンスを書くことは読者の練習として残しておきます。

リストの型構築子である[]は実際のところ二種類の方法でApplicativeのインスタンスにすることができます。それは、リストを順序付けられた要素のコレクションとして扱いたいか、非決定的計算の複数の結果を表す文脈として扱いたいかに依ります。

最初にコレクションの見方から考えてみましょう。特定の型の型クラスのインスタンスはひとつしか存在し得ないので、ひとつ、または両方のリストのApplicativeのインスタンスはnewtypeのラッパーに対して定義する必要があります。たまたま、非決定性計算のインスタンスがデフォルトで、コレクションのインスタンスは、ZipListという名前のnewtypeに関して定義されています。リスト14にこのインスタンスを示します。

newtype ZipList a = ZipList { getZipList :: [a] }

instance Applicative ZipList where
  pure = undefined   -- 練習
  (ZipList gs) <*> (ZipList xs) = ZipList (zipWith ($) gs xs)

リスト14: ZipListのApplicativeインスタンス

(<*>)を使って関数のリストを入力のリストに適用にするには、要素ごとに関数と入力を対応させ、結果の出力のリストを生成します。言い換えると、二つのリストを関数適用である($)で「zip」します。そういうわけで、ZipListという名前なのです。練習として、pureを正しく定義してみてください。リスト13に示される法則を満たす実装はひとつしかありません。

リスト15に、非決定性計算の視点から見た、リストに対するもうひとつのApplicativeのインスタンスを示します。入力のペアに対して関数を適用する代わりに、それぞれの関数を全ての入力に対して順番に適用し、全ての結果をリストに集めます。

instance Applicative [] where
  pure x = [x]
  gs <*> xs = [ g x | g <- gs, x <- xs ]

リスト15: []のApplicativeインスタンス

これで、非決定性計算を自然なスタイルで書くことができるようになりました。3と4を決定的に足すには、もちろん、(+) 3 4と書くことができます。しかし、3の代わりに2か3か4が結果となるような非決定性計算を考えるならば、以下のように書くことができます。

pure (+) <*> [2,3,4] <*> pure 4

もしくは、もっと慣用句的には、以下のように書きます。

(+) <$> [2,3,4] <*> pure 4

他にもいくつかのApplicativeのインスタンスがあります。

  • IOはApplicativeのインスタンスで、あなたが考えるであろうその通りに振舞います。g <$> m1 <*> m2 <*> m3が実行されると、miの副作用が左から右の順で発生します。
  • ((,) a)は、aがMonoidのインスタンスである限りApplicativeです。aの値は、計算と同時に累算されます。
  • ApplicativeモジュールはConst型構築子を定義しています。Const a b型の値は単にaを保持します。この型は、任意のMonoid aに対してApplicativeのインスタンスになります。このインスタンスは、Foldableなどと組み合わせたときに特に便利です。
  • WrappedMonadやWrappedArrow newtypeは、あらゆるMonadやArrowのインスタンスをApplicativeのインスタンスにします。これらの型クラスを学ぶときに見るように、これらの型クラスはそのメソッドを使用してApplicativeのメソッドを実装できるという意味において、厳密にApplicativeよりも表現力があります。
洞察

McBrideとPatersonの論文は、計算文脈における関数適用を表すのに、[[g x1 x2 ... xn]]という記法を導入しました。各xiが何らかのアプリカティブファンクタであるfに対してf tiという型を持ち、gが、t1 -> t2 -> ... -> tn -> tという型を持つならば、[[ g x1 ... xn]]全体はf tという型になります。これは、複数の「副作用のある」引数への関数の適用と考えることができます。この意味で、二重鍵括弧記法は、文脈内でひとつの引数に対して関数を適用することができるfmapの一般化と言えます。

なぜ、このfmapの一般化を実装するのにApplicativeが必要なのでしょうか?fmapを使って、最初の引数x1にgを適用するとします。そうすると、f (t2 -> ... t)という型の何かを得ますが、ここで詰まってしまいます。この文脈内の関数をfmapを使って次の引数に適用することができません。しかし、これはまさに(<*>)ができることなのです。

このことから、理想的な[[g x1 x2 ... xn]]という記法をHaskellに適切に変換すると、

g <$> x1 <*> x2 <*> ... <*> xn

となることがわかります。ここでは、Control.Applicativeがfmapの便利な中記法である(<$>)を定義していることを思い出してください。このことが、「アプリカティブスタイル」の意味するところなのです。つまり、副作用のある計算が、関数適用の形で表せるということです。唯一の違いは、関数適用するために、単に並べるだけではなく、特殊な演算子である(<*>)を使わなくてはいけないことだけです。

更なる読み物

標準ライブラリには、他にもpureと(<*>)を使って実装した沢山の便利なコンビネータがあります。例えば、(*>)、(<*)、(<**>)、(<$)など[11]です。これらの二次的なコンビネータを賢く使うと、Applicativeを使ったコードはずっと読みやすくなります。

McBrideとPatersonのオリジナルの論文[12]は、情報と例、そしてApplicativeと圏論のつながりについての考察の宝庫です。初心者は読み通すのが難しいと思うかもしれませんが、非常に良く動機付けされていて、初心者であってもわかるところだけ読むだけで何かを得ることができるでしょう。

Conal Elliottは、Applicativeの最大の支持者の一人です。例えば、関数的イメージのためのPanライブラリ[14]や、関数的反応プログラミング(FRP)のreactiveライブラリ[15]は、Applicativeを重点的に使っています。彼のブログには実践的なApplicativeの例が沢山あります。McBrideとPatersonの研究を基にして、ElliottはTypeComposeライブラリ[17]も作成しました。このライブラリは、（いくつかある知見の中でも）Applicativeな型は合成に関して閉じていて、よって簡単な型から構築された複合型に対するApplicativeのインスタンスはしばしば機械的に派生させることができるという知見を具体化します。

Parsec解析ライブラリ[18,19]は元々はモナドとして使うようにデザインされましたが、ほとんどの良くある場面で、Applicativeのインスタンスが大きな効果を発揮するために使えます。Bryan O'Sullivanのブログ記事[20]が良い取っ掛かりになります。もし、Monadによってもたらされる更なる力が必要ないのであれば、代わりにApplicativeを使うのは通常良い考えです。

他にもApplicativeの実践的な良い例は、ConfigFileやHSQLライブラリ[21]、formletsライブラリ[22]にも見られます。

Monad

この記事を読んでいるということは、ApplicativeやArrow、Monoidについて聞いたことがなかったとしても、モナドについては間違いなく聞いたことがあるでしょう。なぜモナドはHaskellにおいてそれほど重要なのでしょうか?それにはいくつかの理由があります。

  • 実際、HaskellはモナドをI/Oを行うためのフレームワークとして使うことで、モナドに特別な注目を集めさせているからです。
  • Haskellはまた、モナドのための特別な糖衣構文であるdo記法を提供することで、モナドを有名にしているからです。
  • Monadは、ApplicativeやArrowのようなほかの抽象モデルよりも長い間存在するからです。
  • モナドに関するチュートリアルが沢山あればあるほど、人々はモナドが難しいに違いないと思い、モナドをついに理解したと思った人が更なる新しいモナドのチュートリアル[1]を書くからです。

これらが正しい理由かどうかはあなたが判断してください。

結局、あらゆる誇大広告にもかかわらず、Monadはまた別の単なる型クラスに過ぎません。では、定義を見てみましょう。

定義

リスト16にMonadの型クラスの定義を示します。Monad型クラスはPreludeから、いくつかの標準的なインスタンスと共に公開されています。しかし、多くの便利な関数はControl.Monadにあり、（((->) e)のような）いくつかのインスタンスはControl.Monad.Instancesにあります。

class Monad m where
  return :: a -> m a
  (>>=)  :: m a -> (a -> m b) -> m b
  (>>)   :: m a -> m b -> m b
  m >> n = m >>= \_ -> n

  fail   :: String -> m a

リスト16: Monad型クラス

Monadクラスのメソッドを一つ一つ見ていきましょう。returnの型には馴染みがあるはずですが、pureと同じ型です。実際、returnはpureのことなのですが、不幸な名前を持っています（なぜ不幸かといえば、命令型プログラミングの世界からやってきた人は、実際には類似性はほとんど無いのに、returnは同じ名前のCやJavaのキーワードと同じようなものだと考えるからです）。数学的な見方をすると、あらゆるモナドは、基点付きファンクタ（実際にはアプリカティブファンクタ）ですが、歴史的な理由でMonadクラスの宣言は残念なことにこれらから派生していません。

(>>)はデフォルトの実装のある(>>=)の特別なバージョンだとわかります。(>>)が型クラスの宣言に含まれているのは、Monadの特定のインスタンスがより効率的な実装でデフォルトの実装を置き換えることができるようにするためです。さらに、_ >> n = nは型としては正しい(>>)の実装ですが、意図された意味論に対応していません。つまり、m >> nはmの結果を無視しますが、その副作用は無視しないことを意図しています。

fail関数はMonadクラスにいるべきではないひどいハックです。詳細は後ほど。

本当に興味深いただひとつのことは、Monadを真にPointedやApplicativeより力強くしている(>>=)です。(>>=)はしばしば束縛と呼ばれます。リスト17にMonadの別の定義を示します。

class Applicative m => Monad' m where
  (>>=) :: m a -> (a -> m b) -> m b

リスト17: Monadの別の定義

(>>=)の裏にある洞察についてしばらく時間を割いて話すことができますし、実際にそうしますが、その前にいくつかの例を見てみましょう。

インスタンス

もしあなたがMonadの裏にある洞察について理解していなかったとしても、型の導くままに進めば、インスタンスを作ることができます。このことが実際に洞察を理解する長い道のりに繋がっていることに驚くことでしょう。少なくとも、Monadクラス一般に関して読むのに合わせていじることのできる具体的な例が得られます。最初のいくつかの例は標準Preludeにあります。その他の例はモナド変換ライブラリ(mtl)[24]にあります。

  • 最も単純なMonadのインスタンスはIdentity[25]で、Dan Piponiの強くお勧めするブログ記事である"The Trivial Monad"[26]で述べられています。この記事は、「自明」ではありますが、Monad型クラスへの重要な導入であり、頭を働かせ始めるための良い問題が含まれています。

  • 次に単純なMonadのインスタンスはMaybeです。私たちは既にMaybeに対して、return/pureをどのように書くかを知っています。ではどうやって(>>=)を書くのでしょうか?では、型を考えて見ましょう。Maybeに特化すると、以下の型が得られます。

    (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b

    もし(>>=)への最初の引数がJust xならば、二番目の引数に適用できるa型の何か（すなわちx）を持っていることになります。そして、それはMaybe bとなり、これはまさに私たちが求めていたものです。(>>=)の最初の引数がNothingだったらどうでしょう?この場合、私たちは、a -> Maybe bの関数に適用できるものを何も持っていませんので、できることはひとつしかありません。つまり、Nothingを返します。リスト18にこのインスタンスを示します。既にここで何が行われているかに関するちょっとした洞察が得られています。もし、いくつかの関数を(>>=)でつなげることで計算を作り上げたら、いずれかの計算が失敗したら計算全体が失敗します（なぜなら、Nothing >>= fは、fにかかわらずNothingになるからです）。計算全体は、構成する全ての関数が個別に成功した場合にのみ成功します。というわけで、Maybeモナドは、失敗しうる計算をモデル化します。

    instance Monad Maybe where
  return = Just
  (Just x) >>= g = g x
  Nothing  >>= _ = Nothing

リスト18: MaybeのMonadインスタンス
  • リスト構築子である[]のMonadのインスタンスは、Applicativeのインスタンスに似ています。この実装は練習問題として残しておきます。型に従いましょう!
  • もちろん、IO構築子は有名なモナドですが、その実装はいくらか魔術的で、実際コンパイラごとに異なります。IOモナドだけが魔術的なモナドであるということは、強調する価値があります。IOモナドを使うと、全く純粋な方法で、副作用のある計算を表す値を組み上げることができます。IO型の特別な値であるmainは、ランタイムによって取り上げられ、実際に実行されて、実際の副作用を引き起こします。その他の全てのモナドは関数的に純粋で、特別なコンパイラのサポートを必要としません。しばしばモナド的な値を「副作用のある計算」と言いますが、これはいくつかのモナドが副作用のあるようなコードを書くことを許すからで、実際にはモナドがこれらの明らかな副作用を関数的に純粋な方法で実装するのを隠しているのです。

  • 先に述べたように、((->) e)はリーダーモナドとして知られています。なぜなら、それが型eの値が読み込み専用の環境として存在するような計算をあらわすからです。((->) e)のMonadのインスタンスを自分で書いてみてください。

    Control.Monad.Readerモジュール[27]は、(e -> a)の便利なnewtypeラッパーであるReader e a型と、適切なMonadインスタンス、そしてReader特有の便利な関数を提供しています。それには、ask（環境を取得する）、asks（環境の関数を取得する）、そしてlocal（異なる環境で下位の計算を実行する）が含まれます。

  • Control.Monad.Writerモジュール[28]は、Writerモナドを提供します。このモナドを使うと、計算が進むのにつれて情報を集めることができます。Writer w aは(a, w)と同型で、出力値aが、型wの注釈や「ログ」と共に運ばれます。このとき、型wはMonoidのインスタンスである必要があります。特別な関数であるtellがログを出力します。
  • Control.Monad.Stateモジュール[29]は、s -> (a, s)のnewtypeラッパーであるState s a型を提供します。State s a型の値は、aを生成し、その過程でs型の状態にアクセスしたり、変更したりする状態を持った計算をあらわします。このモジュールはState特有の便利な関数も提供します。それには、get（現在の状態を読む）、gets（現在の状態の関数を読む）、put（状態を上書きする）、そしてmodify（状態に関数を適用する）が含まれます。
  • Control.Monad.Contモジュール[30]は、継続渡しスタイルの計算をあらわすContモナドを提供します。このモナドは、計算を中断、再開したり、局所的でない制御の転送、コルーチン、その他の複雑な制御構造を、関数的に純粋な方法で実装するのに使われます。Contは、その普遍的な属性から「全てのモナドの母」[31]と呼ばれています。
洞察

(>>=)の型をもっと詳しく見てみましょう。基本的にわかることは、(>>=)が二つの計算を一つの大きな計算に結合することです。最初の引数であるm aが最初の計算です。しかし、もし二番目の引数がm bであったならば、計算同士が相互に作用する方法がないことになり、つまらないことになります。そこで、(>>=)の二番目の引数はa -> m bという型をしています。この関数は、最初の計算の結果を渡されると、実行すべき二番目の計算を生成します。言い換えると、x >>= kはxを実行し、xの結果を使って次に実行する計算を決め、その計算の結果を全体の計算の結果として出力します。

直感的に、MonadをApplicativeよりも力強くしているのは、前の計算の出力を次に実行する計算を決定するために使うというこの能力です。Applicative計算の構造は固定されていますが、Monadの計算の構造は途中の結果に応じて変わり得ます。

別の見方からMonadの増加した力を見るために、(>>=)をfmap、 pure、(<*>)を使って実装しようとすると何が起きるか見てみましょう。手元には、m a型の値xと、a -> m b型の関数kがあります。ですから、できることは、kをxに適用することしかありません。もちろん直接適用することはできません。fmapを使ってmに対して持ち上げなくてはなりません。しかし、fmap kの型は何になるでしょうか?それは、m a -> m (m b)になります。これをxに適用すると、m (m b)型の何かが残されます。しかし、ここで詰まってしまいます。実際に欲しいのはm bなのに、ここから得る方法がありません。pureを使ってmを追加することはできますが、複数のmを一つに畳み込む方法はありません。

この複数のmを畳み込む能力が、まさにjoin :: m (m a) -> m a関数によって提供される能力です。そして、リスト19に示すように、別のMonadの定義がjoinによって与えられるのは驚きではないでしょう。

class Applicative m => Monad'' m where
  join :: m (m a) -> m a

リスト19: joinを使ったMonadの別な定義

実のところ、圏論においてモナドは、return、fmap、そしてjoinによって定義されます（しばしば数学的には、η、Τ、μと呼ばれます）。Haskellは同等の数式を定義するのに、joinの代わりに(>>=)を使用します。これは、その方が便利なためです。しかし、時にはMonadのインスタンスをjoinを使って考えた方が、「原始的」なために、簡単なことがあります（例えば、リストモナドのjoinはconcatです）。(>>=)をfmapとjoinを使って実装したり、joinを(>>=)を使って実装するのは良い練習になります。

便利な関数

Control.Monadモジュール[32]はたくさんの便利な関数を提供しますが、その全ては基本的なMonadの操作（特にreturnと(>>=)）で実装されています。私たちは既にそのうちの一つ、joinを見ました。さらにいくつかの注目すべき関数を見てみます。これらを自分で実装してみるのは良い練習になります。これらの関数のもっと詳細なガイドは、Henk-Jan van Tuylのツアー[33]に、コメントや例のコードと共にありますので見てみてください。

  • liftM :: Monad m => (a -> b) -> m a -> m b。これは馴染み深いはずです。もちろん、これはfmapです。fmapとliftMの両方があるという事実は、数学的には全てのモナドがファンクタなのにも関わらずMonadクラスがFunctorのインスタンスを要求しないことの不幸な結果です。しかし、fmapとliftMは原則としてどちらを使っても変わりはありません。なぜなら、MonadのインスタンスなのにFunctorのインスタンスでないのは（技術的というよりは社会的な）バグだからです。
  • ap :: Monad m => m (a -> b) -> m a -> m bもまた馴染み深いはずです。これは、(<*>)と同等で、このことはMonadがApplicativeよりも厳密に力強いという主張を正当化します。あらゆるMonadは、pure = return、(<*>) = apとすることで、Applicativeのインスタンスにすることができます。
  • sequence :: Monad m => [m a] -> m [a]は、計算のリストを、各計算の結果をリストにするような一つの計算にまとめます。sequenceがMonad制約を持つのもまた歴史の偶然で、実際にはApplicativeだけを使って実装することができます。リスト以外の構造に対するsequenceの追加の一般化がありますが、それについてはTraversableの章で議論します。
  • replicateM :: Monad m => Int -> m a -> m [a]は単にreplicateとsequenceの組み合わせです。
  • when :: Monad m => Bool -> m () -> m ()は、条件に応じて計算を実行します。テストがTrueならば二番目の引数を評価し、そうでなければreturn ()します。他のモナド的な条件式のコレクションは、IfElseパッケージ[34]にあります。
  • mapM :: Monad m => (a -> m b) -> [a] -> m [b]は、最初の引数を二番目のリストにマップし、結果をsequenceします。forMは、単にmapMの引数の順番を逆にしたもので、forループを一般化するのでforMと呼ばれます。つまり、リスト[a]がループのインデックスとなり、関数a -> m bが各インデックスに対するループの「本体」となります。
  • (=<<) :: Monad m => (a -> m b) -> m a -> m bは、単に(>>=)の引数の順番が逆になったものです。関数適用により近いため、この向きが便利なことが時々あります。
  • (>=>) :: Monad m => (a -> m b) -> (b -> m c) -> a -> m cは、関数合成のようなものですが、各関数の結果の型にmが付いていて、引数が入れ替わっています。この演算子については後ほどもう少し述べます。
  • guard関数はMonadPlusのインスタンスと共に用いられます。これについては、Monoidの章の最後で議論します。

これらの関数の多くは、sequence_やmapM_のような「アンダースコアの付いた」変化形があります。これらの変化形は引数として渡された計算の結果を捨て、計算の副作用のみを使用します。

法則

Monadのインスタンスが満たさなくてはならないいくつかの法則があります[35]。リスト20に標準的な表記を示します。

return a >>= k = k a
m >>= return   = m
m >>= (\x -> k x >>= h) = (m >>= k) >>= h

fmap f xs = xs >>= return . f = liftM f xs

リスト20: Monadの法則

最初と二番目の法則は、returnが良い感じに振舞うことを表現しています。もし値aをreturnを使ってモナドの文脈に入れ、kに束縛したならば、単に最初からkをaに適用したのと同じです。計算mをreturnに束縛しても何も変わりません。三つ目の法則の述べるところは、本質的には、(>>=)は結合的であるということです。最後の法則は、FunctorでもMonadでもある型（これは既に述べたようにあらゆるMonadのインスタンスがそうであるべきなのですが）に対しては、fmapとliftMは同じものであることを保証します。

しかし、上の法則の見た目は、特に三番目の法則は、(>>=)が非対称であるために台無しになっています。この法則を見て、何を言いたいのか理解するのは困難です。私は(>=>)を使って定式化された、もっと精錬されたバージョンの法則が好みです。(>=>)がa -> m bとb -> m cという型の二つの関数を「合成する」ことを思い出してください。a -> m bの型を、（大雑把に）mに対応する文脈において何らかの副作用を持ったaからbへの関数と考えることができます（returnはそのような関数です）。(>=>)を使うと、このような「副作用のある関数」を合成することができますが、この(>=>)がどのような属性を持つのかを知りたいわけです。リスト21に、(>=>)を使って再定式化されたモナドの法則を示します。

return >=> g = g
g >=> return = g
(g >=> h) >=> k = g >=> (h >=> k)

リスト21: (>=>)を使って再定式化されたMonadの法則

かなり良くなりました。この法則は単に、returnは(>=>)の単位元であり、(>=>)は結合性があると述べています。g >=> h = \x -> g x >>= hという定義のもとで、これらの二つの公式が同じものであることを証明するのは、練習問題にします。

fmap、returnとjoinを使ったモナド則の公式もあります。この公式に関する議論は、Haskell wikibookの圏論のページ[9]を参照してください。

do記法

Haskellの特別なdo記法は、モナド式の連鎖のための糖衣構文を用意することで、「命令的なスタイル」をサポートします。この記法の起源は、a >>= \x -> b >> c >>= \y -> dのようなものを、行を分けて書くことで読みやすくなるということを認識したところにあります。

a >>= \x ->
b >>
c >>= \y ->
d

この書き方をすることで、全体としての計算が、a、b、cとdの四つの計算によって成り立っていて、xはaの結果に、yはcの結果に束縛される（b、cとdはxを参照することができ、dは同様にyを参照することができます）ということが強調されます。ここからもっと良い記法を想像するのはそれほど難しくありません。

do { x <- a ;
     b      ;
     y <- c ;
     d
   }

（波括弧とセミコロンは省略可能です。Haskellのパーサはレイアウトを使ってそれらがどこに挿入されるべきか決定します。）この議論によって、do記法は単なる糖衣構文であることが明確になったはずです。実際、doブロックは、ほとんどリスト22に示されるように、再帰的にモナド演算に変換されます。

　                 do e -> e
　      do { e; stmts } -> e >> do { stmts }
　 do { v <- e; stmts } -> e >>= \v -> do { stmts }
do { let decls; stmts } -> let decls in do { stmts }

リスト22: doブロックの糖衣構文を元に戻す

これですべてではありません。なぜならば、vは変数ではなくパターンかも知れないからです。例えば、以下のように書くことができます。

do (x:xs) <- foo
   bar x

しかし、もしfooが空のリストを生成したら何が起こるでしょうか?Monad型クラスにあった醜いfail関数のことを覚えていますか?それがまさに起こることです。詳細はHaskellレポートの3.14章[3]を参照してください。そして、MonadPlusとMonadZeroについての議論も参照してください。

最後の注意点です。do記法は、「コンテナ」の見方ではなく、「計算の文脈」の見方にとても強く合致しています。なぜなら、x <- mという束縛の記法が、mからひとつのxを「取り出し」、それを使って何かをすることを連想させるからです。しかし、mは、リストや木のような何らかのコンテナを表現しているかもしれません。x <- mの意味は(>>=)の実装に完全に依存しています。例えば、mがリストならば、x <- mにおいて、xはリストから順番に取り出された個々の値を表すことになります。

モナド変換子

しばしば二つのモナドを一つに結合したくなることがあるでしょう。例えば、状態を持った非決定的な計算（State + []）や、読み取り専用の環境を参照する失敗するかも知れない計算（Maybe + Reader）などです。残念ながら、モナドはアプリカティブファンクタのようにうまく合成することができません（これも、Monadの持つすべての力が必要でなければApplicativeを使うべきであるまた一つの理由です）が、いくつかのモナドは何らかの形で結合することができます。

モナド変換子ライブラリ[24]は、StateT、ReaderT、ErrorT、そして（近々）MaybeTのような沢山のモナド変換子を提供しています。これらのモナド変換子に他のモナドを適用することで、両方の副作用を持った新しいモナドを作ることができます。例えば、StateT s MaybeはMonadのインスタンスで、型StateT s Maybe a型の計算は失敗する可能性があり、変更可能なs型の状態にアクセスします。これらの変換子は複数個重ね合わせることができます。モナド変換子を使うときには、合成の順番が重要だということは覚えておかなくてはいけません。例えば、StateT s Maybe aの計算が失敗したとき、状態の更新は停止します。逆に、MaybeT (State s) aの計算の状態は、計算が失敗した後でも変更され続けます（これは逆に見えるかも知れませんが、間違っていません。モナド変換子は合成されたモナドを「裏返しに」構築します。例えば、MaybeT (State s) aは、s -> Maybe (a, s)と同等です。Lambdabotには、欠くことのできない@unmtlコマンドがあり、このコマンドを使って、この方法でモナド変換子を「ほどく」ことができます）。

すべてのモナド変換子は、Control.Monad.Transで定義されたMonadTrans型クラス（リスト23）を実装する必要があります。この型クラスは、基本モナドmにおける任意の計算を、変換されたモナドt mの計算に「もちあげ」られるようにします（型の適用は、関数の適用と同様に左結合なので、t m a = (t m) aです。練習問題として、tの種を考えると良いでしょう。この種はここまでに見たどの種よりもむしろ興味深いものです）。しかし、MonadTransを考える必要があるのは自分のモナド変換子を定義するときだけで、定義されたものを使うときには考える必要はありません。

class MonadTrans t where
  lift :: Monad m => m a -> t m a

リスト23: MonadTrans型クラス

さらにMonadStateのような型クラスもあり、getやputのような状態を扱うためのメソッドを提供します。この型クラスのおかげで、Stateだけでなく、MaybeT (State s)、StateT s (ReaderT r IO)などのような、MonadStateのインスタンスであるようなあらゆるモナドの中で、これらのメソッドを便利に使うことができます。同じような型クラスが、Reader、Writer、Cont、IOなどに対して存在します。

二つのすばらしいモナド変換子に関する参考文献があります。Martin GrabmullerのMonad Transformers Step by Step[37]は、実際に動く例題を伴った、色々な副作用を持った計算を優雅にくみ上げるのにどのようにモナド変換子を使うのかを詳細に述べています。Cale Gibbardのモナド変換子の使い方に関する記事[38]はもっと実践的で、できるだけ楽にコードを書くために、モナド変換子を使ってどのようにコードを構築するかを説明しています。別のモナド変換子を学ぶ取っ掛かりは、Dan Piponiのブログの記事[39]です。

MonadFix

MonadFixクラスは、特別な不動点を求めるmfix :: (a -> m a) -> m aをサポートするモナドについて記述します。これを使うと、モナド計算の出力を再帰を使って定義することができます。これは、GHCとHugsで特別な「再帰的do」記法であるmdoを使ってサポートされています。更なる情報は、Levent Erkokの論文、Value Recursion in Monadic Computations[40]を参照してください。

更なる読み物

Philip Wadlerが、最初に関数型プログラムの構造化にモナドを使うことを提案しました[41]。彼の論文は、このテーマの今でも読みやすい入門書です。

モナド変換子ライブラリ(mtl)[24]は、Reader、Writer、Stateやその他のモナド、そしてモナド変換子フレームワーク自体も含めて、Mark Johnsの古典的な論文であるFunctional Programming with Overloading and Higher-Order Polymorphism[42]に着想を得ています。この論文は、15年経った今なお読む価値があり、そして読みやすいものです。

もちろん、さまざまな質の沢山のモナドのチュートリアルがあります[43,44,45,46,47,48,49,50,51,52]。その中でも良いものには、Cale GibbardのMonads as containers[44]やMonad as computation[51]があります。Jeff NewbernのAll About Monads[43]は沢山の例の載った包括的なガイドです。そして、Don PiponiのYou could have invented monads!はすばらしい練習問題を呼び物にしています。もし、IOの使い方を知りたいだけならば、Introduction to IO[53]が参考になるでしょう。これらは見本として抽出したに過ぎません。もっと完全なリストは、Haskell wiki[54]にあります（これらのモナドチュートリアルは、いくつかのパロディ[55]、そしていくつかの種類の反動[56,1]を作り出しました）。チュートリアルに限らないモナドの良い参考文献には、Henk-Jan van TuylのControl.Monadにある関数のツアー[33]、Don Piponiの「フィールドガイド」[57]、そしてTim NewshamのWhat's Monad?[58]があります。そして、モナドの色々な面について書かれた沢山のブログ記事があります。リンク集はHaskell wiki[59]にあります。

MonadクラスとHaskellの型システムの特異なところのひとつは、仮に数学的に見てモナドであっても、データにクラス制約を必要とする型のMonadのインスタンスを直接的に宣言することができないことです。例えば、Data.SetはデータにOrd制約を必要とするので、簡単にはMonadのインスタンスにはできません。この問題に対する解決方法は、Eric Kiddによってはじめて述べられ[60]、Ganesh SittampalamとPeter Gavin[61]によってライブラリになりました。

do記法を避けるべき妥当な理由が沢山あります。人によっては、それが有害であると考えるようになっています[62]。

モナドは色々な方法で一般化できます。ひとつの可能性としては、パラメータ化されたモナドがあります。Robert Atkeyのこれに関する論文[63]や、Don Piponiの説明[64]を参照してください。

圏論好きにとっては、モナドはモノイドとして見ることができ[65]、クロージャー演算子としてみることもできます[66]。Monad.Readerのこの号にあるDerek Elkinsの記事[67]に、StateとContのような標準Monadインスタンスのいくつかの圏論における基礎が説明されています。モナドを合成するその他の方法として、coproductsを使った方法がLuthとGhani[68]によって説明されていますが、この方法は（まだ?）広く広まっていないようです。

モナドに関するもっと沢山の論文へのリンクが、Haskell wiki[69]にあります。

Monoid

モノイドは、集合Sの要素を結合する二項演算＋を伴った集合Sです。＋演算子は結合的である必要があり（つまり、Sの要素であるあらゆるa、b、cに対して、(a＋b)＋c = a＋(b＋c)）、Sの要素として＋に関して単位元である要素がある必要があります（もし群論に馴染んでいるのならば、モノイドは逆元が必要であるという要件を除いた群です）。例えば、自然数は加算の下でモノイドです。二つの自然数の合計は自然数で、あらゆる自然数a、b、cに対して(a + b) + c = a + (b + c)が成り立ち、ゼロが加算に対して単位元です。また、整数は乗算の下で、自然数はmax演算の下で、真偽値は論理積と論理和の下で、リストは連結の下で、集合からそれ自体への関数は関数結合の下でモノイドです。探し方がわかれば、モノイドはどこにでもあります。

定義

リスト24に（Data.Monoidで定義される）Monoid型クラス[70]の定義を示します。

class Monoid a where
  mempty  :: a
  mappend :: a -> a -> a

  mconcat :: [a] -> a
  mconcat = foldr mappend mempty

リスト24: Monoid型クラス

mempty値がモノイドの単位元要素をあらわし、mappendが二項演算子をあらわします。mconcatのデフォルトの定義は、右畳み込みを使用して、mappendですべてを結合することで要素のリストを「畳み込み」ます。mconcatは、特定のインスタンスがもっと効率的な実装を代わりに提供できるようにするためにMonoidクラスに含まれてます。通常は、デフォルトの定義が問題なく動くので、Monoidのインスタンスを作るときにはmconcatを無視して構いません。

Monoidのメソッドは不幸な名前の付け方をされています。これらの名前は、リストのMonoidインスタンス（そこでは、mempty = []で、mappend = (++)）によって着想を得ていますが、多くのモノイドは連結とは無関係なので誤解を招く恐れがあります[71]。

法則

もちろん、各Monoidインスタンスは数学的な意味でモノイドであるべきで、リスト25に示される法則に従うことを意味します。

mempty `mappend` x = x
x `mappend` mempty = x
(x `mappend` y) `mappend` z = x `mappend` (y `mappend` z)

リスト25: Monoid法則
インスタンス

Data.Monoidでは極めて沢山の興味深いMonoidのインスタンスが定義されています。

  • [a]は、mempty = []、mappend = (++)とするとモノイドです。あらゆるリストx、y、zに対して、(x ++ y) ++ z = x ++ (y ++ z)であり、空リストが単位元である（[] ++ x = x ++ [] = x）ことを確認するのは難しくありません。

  • 既に述べたように、加算と乗算の下であらゆる数値型をモノイドにすることができます。しかし、同じ型に対して二つのインスタンスを持つことができないので、Data.Monoidは二つのnewtypeラッパー、SumとProductを適切なMonoidインスタンスと共に提供しています。

    > getSum (mconcat . map Sum $ [1..5])
15
> getProduct (mconcat . map Product $ [1..5])
120

    この例はもちろん馬鹿げていて、単にsum [1..5]とproduct [1..5]と書くことができます。にもかかわらず、これらのインスタンスは、Foldableを議論するときに見るように、もっと一般化された状況では役に立ちます。

  • AnyとAllは、（各々、論理和と論理積の下において）BoolのMonoidインスタンスを提供するためのnewtypeラッパーです。
  • Maybeには三つのインスタンスがあります。基本的なインスタンスは、aのMonoidインスタンスをMaybe aのインスタンスに持ち上げるものです。残りの二つはFirstとLastというnewtypeラッパーで、mappendは最初の（もしくは最後の）Nothingでないアイテムを選びます。
  • Endo aはa -> aの関数のnewtypeラッパーで、合成の下にモノイドを作ります。
  • Monoidのインスタンスを、追加の構造を持ったインスタンスに持ち上げる方法はいくつかあります。既にaに対するインスタンスがMaybe aに対するインスタンスに持ち上げられるのを見ました。タプルのインスタンスもあります。aとbがMonoidのインスタンスならば、(a, b)もインスタンスです。この場合、aとbに対するモノイドの操作を、明白なペアにした方法で使います。最後に、もしaがMonoidならば、あらゆる型eに対してe -> aという関数の型はMonoidのインスタンスです。特に、g `mappend` hは、gとhの両方を引数に適用し、結果をaのMonoidインスタンスで結合するような関数です。これはとても便利で洗練されたものです[72]。
  • 型Ordering = LT | EQ | GTはMonoidで、mconcat (zipWith compare xs ys)がxsとysの辞書順を計算するような形で定義されます。特に、mempty = EQで、mappendは最も左側にあるEQでない引数（もし両方の引数がEQならばEQ）を返します。これは、関数のMonoidインスタンスと共に、なかなか賢いことをするのに使われます[73]。
  • Map、SetやSequenceを含む、containerライブラリ[8]のいくつかの標準的なデータ構造もMonoidのインスタンスです。

Monoidはまた他のいくつかの型クラスを有効にするのにも使われます。先に述べたように、リスト26に示すように((,) e)をApplicativeのインスタンスにするのにMonoidを使います。

instance Monoid e => Applicative ((,) e) where
  pure x = (mempty, x)
  (u, f) <*> (v, x) = (u `mappend` v, f x)

リスト26: Monoidを使った((,) e)のApplicativeインスタンス

Monoidは同様に((,) e)をMonadにするのにも使われます。これは、Writerモナドとして知られています。既に見たように、WriterとWriterTはそれぞれnewtypeラッパーとこのモナドの変換子です。

MonoidはFoldable型クラスにおいて重要な役割を果たします。

その他のモノイドクラス: Alternative、MonadPlus、ArrowPlus

Alternative型クラス[74]は、リスト27に示すように、モノイドの構造を持つApplicativeファンクタのための型クラスです。

class Applicative f => Alternative f where
  empty :: f a
  (<|>) :: f a -> f a -> f a

リスト27: Alternative型クラス

もちろん、Alternativeのインスタンスはモノイドの法則に従わなくてはなりません。

同様に、リスト28に示すように、MonadPlus[75]はモノイドの構造を持つMonadのためのものです。

MonadPlusのドキュメントは、MonadPlusが「選択と失敗」をサポートするモナドをモデル化することを意図していると述べています。モノイドの法則に加えて、MonadPlusのインスタンスは、mzeroが失敗を意味することを明らかにする、

mzero >>= f = mzero
v >> mzero = mzero

を満たすことを期待されます。mzeroはmplusに関して単位元なので、m1 `mplus` m2はm1かm2が成功した（mzero以外に評価された）ときに成功します。つまり、mplusは選択を表します。guard関数もMonadPlusのインスタンスと共に使うことができます。この関数は、条件が満たされることを要求し、満たされない場合には（mzeroを使って）失敗します。MonadPlusインスタンスの単純な例は[]で、Monoidのインスタンスと全く同じものになります。空のリストが失敗を表し、リストの連結が選択を表します。しかし、一般的には、MonadPlusのインスタンスは、Monoidのインスタンスと同じである必要はありません。Maybeはそのような型の例です。Doug AuclairのMonad.Readerの記事[76]は、MonadPlus型クラスの興味深い使い方の例を伴ったすばらしい紹介です。

class Monad m => MonadPlus m where
  mzero :: m a
  mplus :: m a -> m a -> m a

リスト28: MonadPlus型クラス

mzeroだけを含んだ、失敗を伴ったモナドを表すMonadZeroと呼ばれる型クラスがありました。do記法は、パターンマッチの失敗を処理するために、何らかの失敗の概念が必要です。不幸なことに、MonadZeroは、Monadクラスにfailを追加することで廃止されました。もし私たちが幸運なら、いつの日かMonadZeroが復活し、failは帰るべきところに帰って消え去るでしょう[77]。つまり、パターンマッチを使ったdoブロック（つまり失敗する可能性がある）は、MonadZero制約を必要とするのです。そうでなければ、Monad制約だけが必要とされます。

最後に、リスト29に示すArrowZeroとArrowPlus[78]は、モノイド構造を持ったArrowをあらわします。

class Arrow (~>) => ArrowZero (~>) where
  zeroArrow :: b ~> c

class ArrowZero (~>) => ArrowPlus (~>) where
  (<+>) :: (b ~> c) -> (b ~> c) -> (b ~> c)

リスト29: ArrowZeroとArrowPlus型クラス
更なる読み物

モノイドは最近かなりの注目を受けました。これは、究極的には、多くのHaskellの型クラスの名前（特にモノイド）が理論数学から取られていることに不満を述べたBrian Hurtのブログ記事[79]のおかげです。この記事は、そのことに対する議論や、モノイド一般を議論するhaskell-cafeでの長いスレッド[71]を引き起こしました。

しかし、Monoidに関するいくつかのブログの記事がすぐに続きました。初めに、Dan Piponiが、"Haskell Monoids and their Uses"[80]というすばらしい入門記事を書きました。すぐにHeinrich Apfelmusの"Monoids and Finger Trees"[81]が続きました。この記事は、HinzeとPatersonの2-3フィンガーツリーについての古典的な論文を紹介し、洗練され、一般化されたデータ構造を実装するのに、Monoidをとても賢い方法で使用しました。Dan Piponiはさらに速い逐次的な正規表現のマッチングを実行するためにMonoid（とフィンガーツリー）を使うことに関する二つのすばらしい記事[83,84]を書きました。

同じような話ですが、David Placeの、逐次的な畳み込みを計算するためにData.Mapを改良するという記事は、データ構造を一般化するためにMonoidを使う良い例です。

その他の興味深いMonoidの使用の例としては、洗練されたリストをソートするコンビネータ[73]、断片化された情報をまとめる[86]、そしてChung-Chieh ShanとDylan Thurstonによる難しい組み合わせのパズルを解くためにMonoidを使う一連のすばらしい記事[87,88,89,90]があります。

思いも寄らないかもしれませんが、joinが二項演算の役割を果たし、returnが単位元の役割を果たすと考えると、モナドはある種のモノイドと見ることもできます。Dan Piponiのブログ記事[65]を参照してください。

Foldable

Data.Foldableモジュール[91]で定義されたFoldable型クラスは、合計の値に「畳み込む」ことができるコンテナを抽象化します。この型クラスを使用することで、コンテナに依存しない形でそのような畳み込み操作を書くことができます。

定義

リスト30にFoldable型クラスの定義を示します。

class Foldable t where
  fold    :: Monoid m => t m -> m
  foldMap :: Monoid m => (a -> m) -> t a -> m

  foldr   :: (a -> b -> b) -> b -> t a -> b
  foldl   :: (a -> b -> a) -> a -> t b -> a
  foldr1  :: (a -> a -> a) -> t a -> a
  foldl1  :: (a -> a -> a) -> t a -> a

リスト30: Foldable型クラス

複雑に見えますが、実はFoldableインスタンスにするには、foldMapかfoldrの好きな方ひとつのメソッドを実装する必要しかありません。他のすべてのメソッドはこれらのメソッドを使用したデフォルトの実装があり、おそらくもっと効率的な実装を提供できるようにするためにクラスに含まれています。

インスタンスと例

foldMapの型を見ればそれが何をするのか明らかなはずです。コンテナの中のデータをMonoidに変換する方法（a -> mの関数）とaのコンテナ（t a）があるときに、foldMapはコンテナのすべての中身を走査してすべてのaをmに変換し、それらすべてのmをmappendを使って結合します。リスト31に二つの例を示します。リストのための簡単なfoldMapの実装と、Foldableのドキュメントに示された二分木の例です。

instance Foldable [] where
  foldMap g = mconcat . map g

data Tree a = Empty | Leaf a | Node (Tree a) a (Tree a)

instance Foldable Tree where
  foldMap f Empty = Empty
  foldMap f (Leaf x) = f x
  foldMap f (Node l k r) = foldMap f l ++ f k ++ foldMap f r
    where (++) = mappend

リスト31: foldMapの二つの例

foldr関数はPreludeにあるfoldrと似た型を持っていますが、Preludeのfoldrがリストに対してしか使えないのに対して、もっと一般化されています。

FoldableモジュールはまたMaybeとArrayに対するインスタンスも提供します。更に、標準コンテナライブラリ[8]の多くのデータ構造（例えば、Map、Set、TreeやSequence）も自身のFoldableインスタンスを提供します。

派生された畳み込み

Foldableのインスタンスがあるとき、リスト32に示す例のような一般化されたコンテナに依存しない関数を書くことができます。

-- 任意のコンテナのサイズを計算する
containerSize :: Foldable f => f a -> Int
containerSize = getSum . foldMap (const (Sum 1))

-- 述語を満たすコンテナの要素のリストを計算する
filterF :: Foldable f => (a -> Bool) -> f a -> [a]
filterF p = foldMap (\a -> if p a then [a] else [])

-- コンテナの中の文字列の内、aを含むもののリストを取得する
aStrings :: Foldable f => f String -> [String]
aStrings = filterF (elem 'a')

リスト32: Foldableの例

Foldableモジュールはまた沢山の定義済みの畳み込みを提供します。それらの多くはPreludeで定義されたリストに対してしか使えない同じ名前の関数、concat、concatMap、and、or、any、all、sum、product、maximum(By)、minimum(By)、elem、notElem、findの一般化されたバージョンです。foldやfoldMapと適切なMonoidのインスタンスを使ってこれらの関数の洗練された実装を考えてみるのは楽しいかもしれません。

ApplicativeやMonadのインスタンスと共に働き、コンテナ内の各要素から何らかの計算を生成し、そしてそれらの計算の副作用を実行して結果を捨てる、traverse_やsequenceA_のような一般化された関数があります。Foldableクラスは結果で何をするかを指定するには弱すぎるので、結果は捨て去ることしかできません。一般的に、あらゆるApplicativeやMonadのインスタンスをMonoidにすることはできません。もしモノイド構造を持ったApplicativeやMonad、つまりAlternativeやMonadPlusがあれば、結果を同様に結合することができるasumやmsum関数を使うことができます。これらの関数の詳細については、Foldableのドキュメント[91]を参照してください。

Foldableの操作は常に畳み込まれるコンテナの構造を捨て去ってしまうことに注意してください。もし、Foldable tであるようなt a型のコンテナから始めたとすると、Foldableモジュールで定義されたどの操作の出力にもtは現れることはありません。多くの場合、これはまさに私たちが望んでいることですが、ときどきコンテナの構造を維持したままコンテナに対して一般化された走査をしたいときがあります。まさにこれはTraversableクラスが提供するもので、これについては次の章で議論します。

更なる読み物

Foldableクラスは、論文での形からかなり肉付けされていますが、McBrideとPatersonのApplicativeを紹介する論文[12]に起源があります。

Foldable（そしてTraversable）の興味深い使い方が、Janis Voigtlanderの論文であるBidirectionalization for free![92]にあります。

Traversable

定義

リスト33に、Data.Traversableモジュール[93]で定義された、Traversable型クラスを示します。

class (Functor t, Foldable t) => Traversable t where
  traverse  :: Applicative f => (a -> f b) -> t a -> f (t b)
  sequenceA :: Applicative f => t (f a) -> f (t a)
  mapM      :: Monad m => (a -> m b) -> t a -> m (t b)
  sequence  :: Monad m => t (m a) -> m (t a)

リスト33: Traversable型クラス

見てわかるように、あらゆるTraversableはまた畳み込み可能なファンクタでもあります。Foldableと同様、型クラスの中にはたくさんのものがありますが、インスタンスを作るのは実際にはむしろ簡単で、traverseかsequenceAのいずれかを実装します。他のメソッドはこれらの関数を使ったデフォルトの実装を持っています。デフォルトの実装がどんなものかを考えるのは良い練習です。traverseかsequenceAがあるときに、どうやって他の三つのメソッドを実装しますか?（mapMに関するヒント: Control.ApplicativeはWrapMonadというあらゆるMonadをApplicativeにするようなnewtypeを公開しています。sequence関数はmapMを使って実装できます。）

洞察

Traversableの鍵となるメソッドで、その独特の力の源となっているのはsequenceAです。その型を考えてみましょう。

sequenceA :: Applicative f => t (f a) -> f (t a)

これは次の基本的な疑問に答えてくれます。どんな時に二つのファンクタを入れ替えることができるだろうか?例えば、リストのツリーをツリーのリストにすることはできますか?（答え: 二つの方法でできます。どうやって、またなぜなのかは練習問題にします。もっとやりがいのある質問は、ツリーのリストをリストのツリーにできるかどうかというものです。）

二つのモナドを合成する能力は、ファンクタを入れ替えるこの能力に決定的に依存します。直感的に、もしモナドmとnからM a = m (n a)というモナドを作りたいとしたら、そしてjoin :: M (M a) -> M a、つまりjoin :: m (n (m (n a))) -> m (n a)を実装したいならば、m (m (n (n a)))を得るためにnを入れ替えることができなくてはならず、そうすればmとnに対するjoinを使って型がm (n a)の何かを生成することができます。詳細はMark Jonesの論文[42]を参照してください。

インスタンスと例

どんなTraversableのインスタンスの例があるでしょうか?リスト34に、前のFoldableの章の例で使ったのと同じTree型のインスタンスの例を示します。一緒に示したFunctorのインスタンスと比べてみるのは有益です。

data Tree = Empty | Leaf a | Node (Tree a) a (Tree a)

instance Traversable Tree where
  traverse g Empty        = pure Empty
  traverse g (Leaf x)     = Leaf <$> g x
  traverse g (Node l x r) = Node <$> traverse g l
                                 <*> g x
                                 <*> traverse g r

instance Functor Tree where
  fmap     g Empty        = Empty
  fmap     g (Leaf x)     = Leaf $ g x
  fmap     g (Node l x r) = Node $ (fmap g l)
                                   (g x)
                                   (fmap g r)

リスト34: TreeのTraversableのインスタンスの例

TreeのTraversableとFunctorのインスタンスがほとんど同じであることは明白です。たった一つの違いは、Functorのインスタンスが通常の関数適用を使うのに対し、TraversableのインスタンスではApplicativeの文脈の中で(<$>)と(<*>)を使って適用が行われることです。実は、これはあらゆる型に対して成り立ちます。

あらゆるTraversableファンクタは同時にFoldableでもありFunctorでもあります。このことはクラス宣言を見るだけでなく、これらのクラスのメソッドをTraversableのメソッドだけを使って実装できることからもわかります。fmapとfoldMapをTraversableのメソッドだけを使って実装するのは良い練習になります。その実装は驚くほど洗練されたものです。Traversableモジュールはこれらの実装をfmapDefaultとfoldMapDefaultとして提供しています。

標準ライブラリは沢山のTraversableインスタンスを提供しています。これには、[]、Maybe、Map、TreeとSequenceに対するインスタンスを含みます。注目すべきことに、SetはFoldableではありますが、Traversableではありません。

更なる読み物

TraversableクラスもまたMcBrideとPatersonのApplicativeに関する論文[12]に起源を持ちます。そして、詳細はGibbonsとOliveiraのThe Essence of the Iterator Pattern[94]に述べられています。この論文には、関連する研究への大量の参考文献が含まれています。

Category

Categoryもつい最近Haskell標準ライブラリに追加されたもので、baseパッケージのバージョンによってインストールされているかどうかが変わります。Categoryは、関数合成の概念を一般的な「射」に一般化します。

リスト35に（Control.Category[95]にある）Category型クラスの定義を示します。読みやすいように、中置の関数型構築子(->)に良く似た中置型構築子(~>)を使っています。この記法はHaskell 98の一部ではありません。二番目の定義は標準ライブラリで使われているものです。残りの記事では、CategoryとArrowのために中置型構築子(~>)を使います。

class Category (~>) where
  id  :: a ~> a
  (.) :: (b ~> c) -> (a ~> b) -> (a ~> c)

-- 通常の（前置の）型構築子を使った同じもの
class Category cat where
  id  :: cat a a
  (.) :: cat b c -> cat a b -> cat a c

リスト35: Category型クラス

Categoryのインスタンスは、二つの型引数を取る、つまり種が* -> * -> *な型構築子でなくてはならないことに注意してください。型構築子の変数であるcatを関数構築子(->)で置き換えて考えてみるのも有益です。実はこの場合には、正に標準Preludeにあるおなじみの恒等関数idと関数合成演算子(.)となります。

もちろんCategoryモジュールは正にこのような(->)のCategoryインスタンスを提供しています。しかし、リスト36に示すように、もうひとつのインスタンスも提供しています。そのインスタンスは、Monad法則に関する以前の議論でお馴染みでしょう。Control.Arrowモジュールで定義されたKleisli m a bは、a -> m bの単純なnewtypeラッパーです。

newtype Kleisli m a b = Kleisli { runKleisli :: a -> m b }

instance Monad m => Category (Kleisli m) where
  id = Kleisli return
  Kleisli g . Kleisli h = Kleisli (h >=> g)

リスト36: KleisliのCategoryインスタンス

Categoryインスタンスのたった一つの法則は、idと(.)がモノイドとなることです。つまり、idは(.)の単位元であり、(.)は結合則を満たす必要があります。

最後に、Categoryモジュールは追加の二つの演算子を公開しています。(<<<)は単なる(.)の別名で、(>>>)は引数を反転した(.)です（以前のバージョンのライブラリでは、これらの演算子はArrowクラスの一部として定義されていました）。

更なる読み物

Categoryという名前は少し誤解を招きます。なぜなら、Categoryクラスは任意の圏をあらわすことができず、単にHask圏、つまりHaskellの型の圏を表現できるに過ぎないからです。Haskellでのもっと一般的な圏の扱いについては、category-extrasパッケージ[2]を参照してください。一般的な圏論については、すばらしいHaskell wikibookのページ[9]、Steve Awodeyの新しい本[96]、Benjamin PierceのBasic category theory for computer scientists[97]、またはBarrとWellsの圏論の講義ノート[98]を参照してください。Benjamin Russellsのブログ記事[99]も動機の良い源であり、圏論のリンクもあります。やり手の生産性の高いHaskellプログラマになるのに圏論のことを知っている必要はありませんが、Haskellの下地にある理論を深く正しく理解することに役に立ちます。

Arrow

Arrowクラスは、MonadやApplicativeと同様に、また別の計算の抽象化を表現します。しかし、出力の型しか反映しないMonadやApplicativeとは違い、Arrow計算の型は入力と出力の両方の型を反映します。アローは関数を一般化します。もし、(~>)がArrowのインスタンスならば、b ~> c型の値は入力として型bの値を取り、出力として型cの値を返す計算と考えることができます。(->)のArrowインスタンスにおいては、これは単なる純粋な関数ですが、一般的には、アローは何らかの「副作用のある」計算を表現します。

定義

リスト37に、Control.Arrow[100]におけるArrow型クラスの定義を示します。

class Category (~>) => Arrow (~>) where
  arr :: (b -> c) -> (b ~> c)
  first :: (b ~> c) -> ((b, d) ~> (c, d))
  second :: (b ~> c) -> ((d, b) ~> (d, c))
  (***) :: (b ~> c) -> (b' ~> c') -> ((b, b') ~> (c, c'))
  (&&&) :: (b ~> c) -> (b ~> c') -> (b ~> (c, c'))

リスト37: Arrow型クラス

まず初めに注目すべき点は、Categoryクラスの制約があることです。つまり、恒等アローとアロー合成をただで手に入れられるということです。g :: b ~> cとh:: c ~> dという二つのアローが与えられたとき、二つの合成であるg >>> h :: b ~> dを作ることができます。

既にお馴染みのように、新しいArrowのインスタンスを定義するために書かなくてはいけないメソッドは、arrとfirstだけです。その他のメソッドは、これら二つを使ったデフォルトの実装がされていますが、より効率的な実装で上書きできるようにArrowクラスに含まれています。

洞察

アローのメソッドを順番に見ていきましょう。Ross Patersonのアローに関するページ[101]には、洞察を進めるのに役立つ良い図表があります。

  • arr関数は、任意の関数b -> cを取り、一般化されたb ~> cにします。arrメソッドは、アローは関数を一般化するという主張を、あらゆる関数をアローとして扱えるようにすることで正当化します。arr gは単にgを計算するだけで、（それが特定のアローに対してどのような意味を持つにせよ）「副作用」がないという意味で「純粋」であることを意図しています。
  • firstメソッドはbからcへの任意のアローを(b, d)から(c, d)へのアローにします。つまり、first gはタプルの最初の要素を処理するのにgを使い、二番目の要素を変更せずに素通りさせます。関数に対するArrowのインスタンスでは、もちろんfirst g (x, y) = (g x, y)です。
  • second関数はfirst関数に似ていますが、タプルの要素が入れ替えられています。実のところ、swap (x, y) = (y, x)というswap補助関数を使うことで、firstを使って定義することができます。
  • (***)演算子はアローの「並列合成」です。二つのアローを取って、タプルに対する一つのアローを作ります。その動作は、最初のアローをタプルの最初の要素に適用し、二番目のアローを二番目の要素に適用します。g *** hはgとhの積（だから*）と覚えられます。関数に対するArrowのインスタンスでは、(g *** h) (x, y) = (g x, h y)と定義できます。(***)のデフォルトの実装はfirst、secondと直列アロー合成である(>>>)を使って定義されています。(***)を使ってfirstとsecondをどうやって実装するのかを考えてみるのも良いでしょう。
  • (&&&)演算子はアローの「ファンアウト（扇のように広がる）合成」です。二つのアローgとhを取り、一つの入力をgとh両方の入力として、それぞれの結果をタプルで返すg &&& hという新しいアローを作ります。g &&& hは入力に対してgとhの両方（だから&）を実装すると覚えることができます。関数に対しては、(g &&& h) x = (g x, h x)と定義できます。
インスタンス

Arrowライブラリ自身は二つのArrowインスタンスしか提供していません。両方とも既に見たことがありますが、通常の関数構築子である(->)と、a -> m bの型の関数を任意のMonad mに対してArrowにするKleisli mです。これらのインスタンスをリスト38に示します。

instance Arrow (->) where
  arr g = g
  first g (x, y) = (g x, y)

newtype Kleisli m a b = Kleisli { runKleisli :: a -> m b }

instance Monad m => Arrow (Kleisli m) where
  arr f = Kleisli (return . f)
  first (Kleisli f) = Kleisli (\ ~(b, d) -> do c <- f b
                                               return (c, d))

リスト38: (->)とKleisli mに対するArrowインスタンス
法則

Arrowのインスタンスが満たさなくてはならない法則はたくさんあります[102,103,104]が、それをリスト39に示します。リスト39に示したバージョンの法則は、上の最初の二つの参考文献に述べられている法則とは少し違うことに注意してください。これは、法則の内のいくつかはCategoryの法則で既に定義されているからです（特にidが恒等アローであることと、(>>>)が結合性であるという要件に注意してください。）。ここに示した法則は、Categoryクラスを使った、Paterson[104]で示された法則に従っています。

　                     arr id = id
　                arr (h . g) = arr g >>> arr h
　              first (arr g) = arr (g *** id)
　            first (g >>> h) = first g >>> first h
　 first g >>> arr (id *** h) = arr (id *** h) >>> first g
　        first g >>> arr fst = arr fst >>> g
first (first g) >>> arr assoc = arr assoc >>> first g

assoc ((x, y), z) = (x, (y, z))

リスト39: Arrow法則

アローを使ってプログラムを書くためにArrow法則を理解するするのは必須ではありませんので、Arrow法則についてそんなに心配することはありません。ArrowChoice、ArrowApply、そしてArrowLoopのインスタンスが満たさなくてはならない法則もいくつかあります。興味のある読者は、Paterson[104]を参照してください。

ArrowChoice

Arrowクラスを使って構築した計算は、Applicativeクラスを使って構築した計算と同様、どちらかというと柔軟性がありません。つまり、計算の構造が初めから決まっていて、途中の結果によって複数の実行パスから選択することができません。ArrowChoiceクラスは正にこの能力を提供します。リスト40にArrowChoiceクラスを示します。

class Arrow (~>) => ArrowChoice (~>) where
  left  :: (b ~> c) -> (Either b d ~> Either c d)
  right :: (b ~> c) -> (Either d b ~> Either d c)
  (+++) :: (b ~> c) -> (b' ~> c') -> (Either b b' ~> Either c c')
  (|||) :: (b ~> d) -> (c ~> d) -> (Either b c ~> d)

リスト40: ArrowChoice型クラス

ArrowChoiceをArrowと比較すると、left、right、(+++)、(|||)と、first、second、(***)、(&&&)の間に明らかな相似形を見ることができます。実際、それらは双対になります。first、second、(***)と(&&&)は、すべて積型（タプル）に対する操作で、left、right、(+++)と(|||)は対応する操作を和型に対して提供します。一般的に、これらの操作は、LeftかRightによってタグ付けされた入力に対して働き、これらのタグによってどう動作するかを選択するアローを作成します。

  • もしgがbからcへのアローなら、left gはEither b dからEither c dへのアローです。Leftでタグ付けされた入力に対しては、left gはgの振る舞いをします。Rightでタグ付けされた入力に対しては、恒等として振舞います。
  • right関数はもちろんleftの反対です。right gアローは、Rightでタグ付けされた入力に対してgの振る舞いをします。
  • (+++)演算子は「多重化」をします。g +++ hは、Leftでタグ付けされた入力に対してgの振る舞いをし、Rightでタグ付けされた入力に対してhの振る舞いをします。タグは保存されます。(+++)演算子は、(***)が二つのアローの積であるのと同様、二つのアローの和（だから+）です。
  • (|||)演算子は「併合」または「ファンイン」です。アローg ||| hは、Leftでタグ付けされた入力に対してgの振る舞いをし、Rightでタグ付けされた入力に対してhの振る舞いをします。しかし、タグは捨て去られます（だから、gとhは同じ出力型を持っていなくてはなりません）。g ||| hは入力に対してg「または」hを実行する、と覚えると良いでしょう。

ArrowChoiceクラスは、途中の結果によって有限の数の実行パスから計算を選択することを許可します。可能性のある実行パスは前もって知られていなくてはならず、(+++)と(|||)で構築されていなくてはいけません。しかし、時にはもっと柔軟性が必要なことがあります。途中の結果からアローを計算し、その計算されたアローを使って計算を続けたいことがあるのです。これが、ArrowApplyによってもたらされる力です。

ArrowApply

ArrowApply型クラスをリスト41に示します。

class Arrow (~>) => ArrowApply (~>) where
  app :: (b ~> c, b) ~> c

リスト41: ArrowApply型クラス

もし、何らかの事前の計算の出力としてアローを計算していたとしたら、appを使うことで、そのアローを入力に対して適用し、その出力をappの出力とすることができます。練習として、別の「カリー化された」バージョンであるapp2 :: b ~> ((b ~> c) ~> c)を実装してみるとよいでしょう。

新しい計算を計算することができるというこの概念にはなじみがあるかもしれません。これは、正にモナドの結合演算子である(>>=)が行っていることです。ArrowApplyとMonadが全く同等の表現力を持つことはそれほど驚きではありません。特に、Kleisli mはArrowApplyのインスタンスにすることができ、ArrowApplyのあらゆるインスタンスは（ArrowMonadというnewtypeラッパーを使って）Monadにすることができます。練習として、リスト42に示すこれらのインスタンスを実装してみましょう。

instance Monad m => ArrowApply (Kleisli m) where
  app = -- 練習

newtype ArrowApply a => ArrowMonad a b = ArrowMonad (a () b)

instance ArrowApply a => Monad (ArrowMonad a) where
  return               = -- 練習
  (ArrowMonad a) >>= k = -- 練習

リスト42: ArrowApplyとMonadの同等性
ArrowLoop

リスト43にArrowLoop型クラスを示します。この型クラスは結果を計算するのに再帰を使うことのできるアローを表現し、（以下で述べる）アロー記法のrec構造を脱糖するのに使われます。

それ自体、loopメソッドの型からはたいしたことはわからないように見えます。しかし、その意図は、一緒に示されたtrace関数の一般化にあるのです。最初のアローの出力のdの成分が自身の入力として戻されています。言い換えると、loop gというアローはgに対する入力の二番目の成分を「固定する」ことで得られます。

class Arrow a => ArrowLoop a where
  loop :: a (b, d) (c, d) -> a b c

trace :: ((b, d) -> (c, d)) -> b -> c
trace f b = let (c, d) = f (b, d) in c

リスト43: ArrowLoop型クラス

trace関数が何をするのか理解するのは少し難しいかもしれません。なぜdがletの左側と右側の両方に現れるのでしょう?これが、Haskellの遅延性の働きです。完全な説明をするスペースがありませんので、興味のある読者は標準のfix関数を勉強し、Patersonのアローのチュートリアル[104]を読んでください。

アロー記法

アロー結合子を直接使ってプログラムを書くのは、特に沢山の途中の結果を同時に参照しなくてはならない場合には、苦痛です。アロー結合子しかなければ、そのような途中の結果はネストされたタプルの中に保持されなくてはなりません。さらに、どの途中結果がどのコンポーネントにあるか覚えて、入れ替えたり、関連付けしなおしたり、必要に応じてタプルの形を変化させるのはプログラマにゆだねられています。この問題は、GHCによってサポートされている特別なアロー記法によって解決されます。これは、モナドのdo記法と似ていて、アローの計算を構築する際に、途中の結果に名前を割り当てることができるようにします。リスト44に、Paterson[104]から取ったアロー記法を使った例を示します。このアローは、リセット線を持つ再帰的に定義されたカウンター回路を表現することを意図しています。

アロー記法について完全な説明をするスペースがここにはありません。興味のある読者は、この記法を紹介するPatersonの論文[105]や、簡単にしたバージョンを紹介する彼のチュートリアル[104]を参照してください。

class ArrowLoop (~>) => ArrowCircuit (~>) where
  delay :: b -> (b ~> b)

counter :: ArrowCircuit (~>) => Bool ~> Int
counter = proc reset -> do
            rec output <- idA     -< if reset then 0 else next
                next   <- delay 0 -< output + 1
            idA -< output

リスト44: アロー記法を使ったアローの例
更なる読み物

アローを学ぶ上ですばらしい出発点となるのは、Patersonによってまとめられたウェブページ[101]で、このページには紹介と沢山の参考文献が含まれています。アローに関する重要ないくつかの論文としては、アローを紹介するHughesのオリジナルの論文であるGeneralising Monads to Arrows[102]と、アロー記法に関するPatersonの論文[105]が挙げられます。HughesとPatersonは後により広い人々に向けてわかりやすいチュートリアルを書きました[104,106]。

HughesのArrowクラスを定義した目的はMonadを一般化することで、Arrowは力としては「ApplicativeとMonadの間」に位置すると言われてきましたが、それらは直接比較することはできません。Lindley、WadlerとYallop[107]が分析するまで、正確な関連性についてはいくつかの混乱がありました。彼らは、ラムダ計算論に基づいてアローの計算論を発明しましたが、それはアロー法則の表現を驚くべきほど単純にしました[103]。

Arrowのいくつかの例としては、Yampa[108]、the Haskell XML Toolkit[109]、そして関数型GUIライブラリであるGrapefruit[110]が挙げられます。

アローへのいくつかの拡張が研究されています。例えば、一方方向ではなく両方向の計算のためのAlimarineらのBiArrow[111]などがあります。

Arrowに関する沢山の論文へのリンクがHaskell wiki[69]にあります。

Comonad

私たちが研究する最後の型クラスはComonadです。ComonadクラスはMonadの圏的双対です。つまり、ComonadはMonadに似ていますが、すべての関数の矢印がひっくり返っています。この型クラスは実際には標準Haskellライブラリには含まれていませんが、最近いくつかの興味深い利用が見られるため、完全を期してここに含めました。

定義

リスト45にcategory-extrasライブラリ[2]のControl.Comonadモジュールで定義されたComonad型クラスを示します。

class Functor f => Copointed f where
  extract :: f a -> a

class Copointed w => Comonad w where
  duplicate :: w a -> w (w a)
  extend :: (w a -> b) -> w a -> w b

リスト45: Comonad型クラス

お分かりのように、extractはreturnの双対で、duplicateはjoinの双対、extendは（引数の順番が違いますが）(>>=)の双対です。Comonadは少し冗長に定義されています（Monadクラスは冗長にならないようjoinを定義から外してるのに）。これはComonadがfmap、extractと、duplicateまたはextendのいずれかによって定義できるようにするためです。それぞれは、もう一方を使ったデフォルトの実装を持っています。

リスト46にComonadのインスタンスの原型的な例を示します。

-- 無限の遅延ストリーム
data Stream a = Cons a (Stream s)

instance Functor Stream where
  fmap g (Cons x xs) = Cons (g x) (fmap g xs)

instance Copointed Stream where
  extract (Cons x _) = x

-- 'duplicate'はリスト関数の'tails'に似ています
-- 'extend'はn番目の要素が元のストリームの
-- n番目よりも前のすべての関数として計算されるように、
-- 元のストリームから新しいストリームを計算します。
instance Comonad Stream where
  duplicate s@(Cons x xs) = Cons s (duplicate xs)
  extend g s@(Cons x xs)  = Cons (g s) (extend g xs)
                       -- = fmap g (duplicate s)

リスト46: StreamのComonadインスタンス
更なる読み物

Dan Piponiはブログの記事でセルオートマトンがどのようにコモナドと関係するのかを説明しています[112]。別のブログ記事では、Conal Elliottが関数型リアクティブプログラミングのコモナド的な定式化について研究しました[113]。Sterling CloverのComonads in everyday lifeというブログ記事[114]は、コモナドとジッパーの間の関係と、コモナドがどのようにウェブサイトのメニューシステムをデザインするのに使われうるのかについて説明しています。

UustaluとVeneはコモナドと関数型言語に関するアイディアを研究する沢山の論文を書いています[115,116,117,118,119]。

謝辞

私に標準Haskell型クラスについて教えてくれた方々、そしてそれらに関する洞察をするのを助けてくれた方々に感謝します。特に、Jules Bean (quicksilver)、Derek Elkins (ddarius)、Conal Elliott (conal)、Cale Gibbard (Cale)、David House、Dan Piponi (sigfpe)、and Kevin Reid (kpreid)に感謝します。

またこの記事のドラフトに沢山の役に立つ反応や提案をしてくれた沢山の方々に感謝します。David Amos、Kevin Ballard、Reid Barton、Doug Beardsley、Joachim Breitner、Andrew Cave、David Christiansen、Gregory Collins、Mark Jason Dominus、Conal Elliott、Yitz Gale、George Giorgidze、Steven Grady、Travis Hartwell、Steve Hicks、Philip H¨olzenspies、Edward Kmett、Eric Kow、Serge Le Huitouze、Felipe Lessa、Stefan Ljungstrand、Eric Macaulay、Rob MacAulay、Simon Meier、Eric Mertens、Tim Newsham、Russell O’Connor、Conrad Parker、Walt Rorie-Baety、Colin Ross、Tom Schrijvers、Aditya Siram、C. Smith、Martijn van Steenbergen、Joe Thornber、Jared Updike、Rob Vollmert、Andrew Wagner、Louis Wasserman、and Ashley Yakeley、そしてIRCのニックネームしか知らない小数の方々、b jonas、maltem、tehgeekmeister、zimanに。間違いなく何人かの名前をうっかり忘れてしまっていると思いますが、感謝の気持ちは変わることはありません。

最後に、Monad.Readerを編集してくれるWouter Swierstraのすばらしい仕事ぶりと、Typeclassopediaを書いている間我慢してくれた私の妻のJoyiaに感謝します。

著者について

Brent Yorgey[120,121]は、ペンシルバニア大学[122]のプログラミング言語グループの博士課程一年生です。彼は教えることやEDSLを作成すること、バッハのフーガを演奏すること、圏論について熟考すること、そして、#haskellの住人においしいラムダのご馳走を振舞うことを楽しんでいます。

参考文献

本日のツッコミ(全25件) [ツッコミを入れる]
# [1..100]>>=pen (2009-10-20 10:57)

量が多いので取り敢えずとびとびで読みました。<br>じっくり読んで気づいた点があったらまた報告します。<br><br>> Monadを真にPointedやApplicativeやより力強くしている<br>typo 「やより」<br><br>> Haskellは、その方が便利なので、joinの代わりに(>>=)を使って<br>> 定義した同じ数式を使用します。<br>「Haskellはjoinを使った構成と同値な構成ができる(>>=)を使います。<br>その方が使いやすいからです。」<br><br>> 多くのモノイドは付け足しとは無関係なので<br>「付け足し」=>「連結」<br><br>> mzeroはmplusの恒等なので、<br>「mzeroはmplusに関して単位元なので」<br><br>> Categoryクラスは任意の圏をあらわすことができず、単に対象がHask、<br>> つまりHaskellの型の圏の圏を表現できるに過ぎないからです。<br>「単に Hask圏、つまりHaskellの型の圏を表現できるに過ぎないからです。」<br><br>> Comonadの定義は少し冗長です（結局、Monadクラスはjoinを必要としません）が、<br>> これは...のいずれかによって定義できるからです。<br>「Comonadは少し冗長に定義されています（Monadクラスは冗長にならないようjoinを外してるのに）。<br>これは...のいずれかによって定義できるようにです。」

# snak (2009-10-20 13:33)

ご指摘ありがとうございます。二番目を除いてほとんどそのまま反映させました。<br><br>二番目は、「Haskellは同等の数式を定義するのに、joinの代わりに(>>=)を使用します。これは、その方が便利なためです。」にしてみました。"equivalent formulation"が、圏論においてモナドを定義する式と同等な式（つまりMonadの型クラスの定義）と考えると、こっちの方がしっくりくるかなと感じたので。そもそもその解釈が間違っているという場合には、教えてください。

# h (2009-10-20 22:24)

翻訳、ありがとうございます。<br><br>本質的な部分ではない指摘で恐縮ですが、MonadとArrowApplyを繋ぐ矢印が「二重の実線の矢印」と表現されていますが、図を見た限りでは、両方向、双頭、若しくは両頭 の実線の矢印という言い方が適している気がしました。

# snak (2009-10-21 00:32)

ご指摘ありがとうございます。「双頭の実践の矢印」に直しました。

# snak (2009-10-21 00:35)

コメントにtypoが…「双頭の実線の矢印」です。

# 山本和彦 (2009-10-28 02:48)

よい記事を訳して頂いてありがとうございます。<br>ざっと読んで気がついた誤植は以下の通りです。<br>「この記事に目的は」→「この記事の目的は」<br>「得ること、もまた」→「得ることも、また」<br>『「副作用のある」な計算」→『「副作用のある」計算』<br>「あ挙げられます」→「が挙げられます」

# snak (2009-10-28 04:16)

ご指摘ありがとうございます。修正しました。

# heita (2009-11-01 05:10)

原著からですが、文献[37]がリンク切れみたい。ググれば一発なので、わざわざ修正することもないかもしれませんが、現在は<br>http://www.grabmueller.de/martin/www/pub/Transformers.en.html<br>で読めます。

# [1..100]>>=pen (2009-11-02 17:57)

typo系<br>「((,) e)はe型の「注釈」を実際の値と共に保持するコンテナを*現し*ます」<br>「関数をコンテナの「内部」に*適用にして*新しいコンテナを生成します」<br>「*リスト10*は、Control.Applicativeで定義されている」=> リスト11<br>「fmapはApplicativeのメソッドを使って実装することができ*まので*」<br>「Writer w aは(a, w)と同型で、出力値aが、Monoidのインスタンスである*必要がる*」<br>「可能性のある実行パスは前もって知られていなくては*いけず*」=> ならず

# [1..100]>>=pen (2009-11-02 18:07)

Monoidのところで出てくるすべての「恒等」とCategoryに出てくる<br>「Categoryインスタンスのたった一つの法則は、... idは(.)の恒等であり」<br>のところだけの「恒等」は「単位元」。

# snak (2009-11-03 03:10)

ご指摘ありがとうございます。すべて反映させました。<br><br>「Writer w aは(a, w)と同型で、出力値aが、Monoidのインスタンスである*必要がる*」のところは読みにくいので文を分けました。

# [1..100]>>=pen (2009-11-03 04:25)

> このライブラリは、Applicativeな型は...見解を具体化します。<br>「このライブラリは（論文の？）知見を具体化しています。その知見とは（中でも）、Applicativeな型は合成に関して閉じていて、よって簡単な型から複合された型に対するApplicativeのインスタンスはしばしば機械的に派生させられるというものです。」

# [1..100]>>=pen (2009-11-03 04:34)

> Functor制約は、我々を正直にさせるのです。<br>「Functor制約（「Functor f =>」のこと）が付いているので（Functor でない型を Applicative として宣言するような）ごまかしはできません。」

# [1..100]>>=pen (2009-11-03 04:44)

> x >>=kはxを実行し、... 二番目の計算を出力します。<br>「x >>=kは、xを実行し、xの結果を使って次に実行する計算を決め、その計算の結果を全体の計算の結果として出力します。」

# [1..100]>>=pen (2009-11-03 07:34)

「モノイドは、集合Sの要素を結合する*ニ項*演算＋を伴った」=><br>二項の二がかたかなの「ニ」になってる（笑）<br>「自然数は*最大値*の下で」=> 「max演算」の方がよいか。

# snak (2009-11-03 16:14)

またまたありがとうございます。<br><br>>> このライブラリは、Applicativeな型は...見解を具体化します。<br>> 「このライブラリは（論文の？）知見を具体化しています。<br>> その知見とは（中でも）、Applicativeな型は合成に関して<br>> 閉じていて、よって簡単な型から複合された型に対する<br>> Applicativeのインスタンスはしばしば機械的に派生させら<br>> れるというものです。」 <br><br>文を分割すると最初の文がなんだかよくわからなくなるので、「このライブラリは、（いくつかある知見の中でも）Applicativeな型は合成に関して閉じていて、よって簡単な型から構築された複合型に対するApplicativeのインスタンスはしばしば機械的に派生させることができるという知見を具体化します。」としました。この手の文は、英語の方が結論が先に来るので読みやすいです。<br><br>> 「Functor制約（「Functor f =>」のこと）が付いているので<br>> （Functor でない型を Applicative として宣言するような）<br>> ごまかしはできません。」 <br><br>この部分はいまいちすっきりしないのでもう少し考えさせてください。というのは、その直前で、Applicativeのメソッドを使ってfmapを実装できるのだから、好む好まざるに関わらずApplicativeはFunctorである、と言っているので、ごまかしができるかどうかという話なのかなという疑問があるのです。どちらかというと、Functor制約があることで、前の文で主張していることを型宣言として明確にしている、ということを言っているのかと思っています。元の訳は確かに意味不明なのですけど…<br><br>他の二つはほぼそのまま反映させました。

# [1..100]>>=pen (2009-11-06 12:29)

「もしくは、もっと*慣習的*に、以下のように書きます」=>「慣用句的に」<br>「これらの型クラスは厳密に ... メソッドを実装することができます」=><br>「これらの型クラスはそのメソッドを使用してApplicativeのメソッドを実装することができるという意味において厳密にApplicativeよりも表現力があります」<br>「fmapとliftMは原則として*交換*可能です」=>「代替」の方がよいか？<br>「*いくつかの*賢いことをするのに使われます」=>「なかなか」「とても」？<br>「モノイドは最近*受けるべき*注目を受けました」=>「多くの」？<br>「構造化されていない情報を集める」=>「断片的な情報をまとめる」<br>「結果は捨て去られる必要があります*」=>「結果は捨て去るしかありません」ぐらいがよい？<br>Arrowの法則「arrid = id」=>「arr id = id」

# snak (2009-11-07 23:51)

少し言葉を変えてほぼ反映しました。ありがとうございます。<br><br>前回ご指摘いただいたApplicativeの件も、直前の文ではなくて、さらにその前の文につながっていると考えると納得がいくので、（注釈は除いて）反映させました。

# konn (2009-11-14 05:25)

すばらしい記事をありがとうございます！<br><br>Traversableの章の洞察の節ですが、<br><br>> sequenceA :: Applicative f => (a -> f b) -> t a -> f (t b)<br><br>となっていますが、<br><br>> sequenceA :: Applicative f => t (f a) -> f (t a)<br><br>のまちがいではないでしょうか。

# ると (2009-11-14 14:44)

リスト37, 39に(:(:))というのが混ざっていますが、これはtypoではないでしょうか。

# snak (2009-11-14 15:49)

konnさん、るとさん、ご指摘ありがとうございます。修正しました。

# Life (2009-11-15 15:54)

翻訳、ありがとうございます！<br>とても助けになりました。<br><br><br>また、本質的な指摘ではありませんが、<br>リスト9: Pointed型クラス において、<br><br>> pure :: a -> f a -- またの名を、signleton, return, unit, point<br><br>とありますが、<br>「signleton」ではなく、「singleton」だと思います。

# fubabz (2009-11-17 10:26)

有用な記事の翻訳ありがとうございます．自分にはまだまだ難解なのですが，以下のtypoをみつけました．<br><br>リスト24 のMonoid定義で型変数が抜けている<br>class Monoid a where

# snak (2009-11-17 14:53)

ありがとうございます。修正しました。

# actorbug (2012-01-11 14:50)

今更ではありますが、typoを見つけたのでご報告します。 <br> <br>Monad 定義 <br>> (>>) :: m a <br>　↓ <br>> (>>) :: m a -> m b -> m b <br> <br>Monad インスタンス <br>> 少なくとも、Monadクラス一般に関して読むのに合わせていじることのできる具体的な例が*得られるます*。 <br>　↓ <br>> 得られます。 <br> <br>Monoid インスタンス <br>> 最後に、もしaがMonoidならば、あらゆる型eに*大して*e -> aという関数の型はMonoidのインスタンスです。 <br>　↓ <br>> 対して <br> <br>Monoid その他のモノイドクラス: Alternative、MonadPlus、ArrowPlus <br>> v >>= mzero = mzero <br>　↓ <br>> v >> mzero = mzero <br> <br>Arrow 洞察 <br>> arrメソッドは、アローは関数を一般化すると*いういう*主張を、あらゆる関数をアローとして扱えるようにすることで正当化します。 <br>　↓ <br>> いう

トップ «前の日記(2009-10-18) 最新 次の日記(2009-11-01)»
This Diary is Running on tDiary.Net 2nd. Powered by fdiary.net.
Generated by tDiary version 3.1.1.20120108
Powered by Ruby version 1.9.3-p0